Das Dreikörper Problem der Schwerkraft Teil 2 - Ellipsen In Teil 1 hatten wir das Szenario zum besseren Verständnis sehr einfach dargestellt, um zu zeigen, daß Hebelgesetze auch bei der Wirkung der Schwerkraft gelten. Eine Kreisbahn definiert sich immer über eine gleichförmige Winkelgeschwindigkeit, damit gilt v = konstant, |Δv| = 0. Jetzt erweitern wir den Ansatz aus Teil 1 auf Ellipsen. Aber keine Angst, es soll weiterhin für jeden verstehbar bleiben, d.h. mit so wenig Mathe wie möglich. Bereits schon mehrfach wurde von Anderen bewiesen, dass eine Ellipse den Weg eines Planeten um eine Sonne beschreibt. Ich möchte in diesem Zusammenhang nur auf die schönen geometrischen Beweise von I.Newton und R.Feynman verweisen. In der verschollenen Vorlesung z.B. beweist R.Feynman geometrisch |Δv| = konstant für elliptische Bahnen, ein toller Beweis zum unbedingt Nachmachen. Aber was ist an Ellipsen so besonderes? Nun, die Ellipsen, die wir betrachten wollen sind Kreise mit zwei verschiedenen, senkrecht aufeinander stehenden Radien. Eine Ellipse ist nichts anderes, als ein Kreis mit Radius r1, der um eine Achse durch M0 gedreht und per rechtwinkliger Projektion auf die Kreisebene zurück übertragen wird, was den kürzeren Radius r2 ergibt. Die Abhängigkeit von den beiden unterschiedlichen Radien geht als quadratische Mittlung ein. Neben dem Mittelbrennpunkt M0 entstehen zwei zusätzliche Brennpunkte M1 und M2, die spiegelsymmetrisch mit einem Abstand von jeweils e = √(r12 - r22) entlang der langen Halbachsen r1 liegen. Alle Geraden durch einen dieser Brennpunkte M1 oder M2 spiegeln sich mit einer einzigen Reflektion an der Ellipsenkurve im anderen Brennpunkt (Einfallswinkel = Ausfallswinkel). Alle Geraden durch den Mittelbrennpunkt M0 reflektieren sich wieder dorthin zurück (mehrfache Reflektion). Alle innerhalb der Ellipse symmetrisch zu M0 angeordneten Punktepaare haben auch diese paarweise Spiegeleigenschaft der Reflexion ineinander vom Kreis geerbt. Kreise mit einem Radius rs < r22 / r1 können innen tangential ganz herumlaufen, ohne irgendwo die Ellipse zu schneiden, denn die Scheitelkrümmung ist genau rs. Und man kann auch zeigen, dass eine gerade Strecke, ein um 90° gedrehter, projizierter Kreis ist :-) Bild 1: Ellipse mit Mittel- und Brennpunkten Aber warum erzähle ich das alles? Nun, diese drei Brennpunkte sind wichtig für einen langfristig stabilen Orbit. Beim Kreis gibt es nur die eine Auswahl, den Mittelpunkt, um den Orbit anzusetzen. Man kann leicht nachweisen, dass ein Kreisorbit, der sich nicht um den Mittelpunkt dreht, nur mit einem Antrieb zu realisieren ist, aber nicht im ballistischen Flug. Kreisorbits sind daher sehr stabil. Die Ellipse bietet stabile Drehpunkte auf der ganzen Linie von M1 über M0 nach M2, die bei Störung der ballistischen Bahn bevorzugt auf die drei Brennpunkte "einrasten", von denen die äußeren Brennpunkte energetisch tiefer liegen und stabiler sind, als der Mittelpunkt, der die doppelte Frequenz hat. Und was ist nun bei Ellipsenbahnen anders? Schauen wir uns dazu noch einmal das Beispiel aus Teil 1 an, die zwei gleich schweren Sonnen, die sich umkreisen und um den Balance-Drehpunkt F0 drehen. 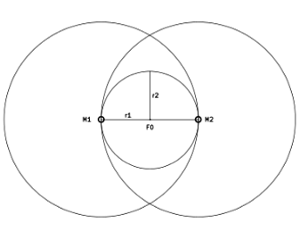Bild 2: Sonne umkreist Sonne aus Teil 1 Jetzt vergrößern wir einfach mal die Länge von r2. Damit laufen die beiden Sonnen bereits auf einer elliptischen Bahn umeinander. Ansonsten bleibt alles wie gehabt, nur dass die Geschwindigkeit der Sonnen größer wird, wenn sie sich nähern (r1) und wieder abnimmt, wenn sie auseinander laufen (r2). Damit ist jetzt klar, was den Unterschied zur Kreisbahn ausmacht. Bei Ellipsenbahnen ist die Geschwindigkeit v die Vermittlung zwischen den zwei unterschiedlichen Radien. Aus den oben erwähnten geometrischen Beweisen wurde eine Flächenregel abgeleitet, die besagt, dass in gleichen Zeitabschnitten immer gleich große Flächen überstrichen werden, v und r also direkt in Beziehung stehen. Gleich große Massen drehen sich, wie in diesem Beispiel, bevorzugt auf der gleichen Bahn um den Brennpunkt M0. Bild 3: Sonne umkreist Sonne auf elliptischer Bahn Das ist der einfachere Fall von zwei Sonnen, beide auf derselben Bahn. Man kann sich das so vorstellen, dass sich 2 Kinder gegenüber aufstellen, sich an beiden Händen überkreuzt halten und zusammen um die Mitte drehen. Wenn eins das andere weiter zu sich herzieht, wird die Drehung schneller, sind die Arme von beiden aber ganz ausgestreckt ist die Drehung am langsamsten. Das kann jeder selber ausprobieren! Die zwei Sonnen haben allerdings keine Arme, sondern nur die Schwerkraft, die sie hält. Auf ihrer Bahn um F0 müssen sie sich genau gegenüber stehen, um sich in ewiger Balance gegenseitig zu umkreisen, d.h. sie brauchen immer einen Phasenversatz von exakt 180°. Jetzt kommen wir zu einer komplizierteren Frage. Eine der beiden gleich schweren Sonnen soll eine eigene Ellipsenbahn durchlaufen. Was ist dann mit der Bahn der anderen Sonne? Nun, wir erinnern uns kurz an Actio = Reactio und wissen, dass das dann auch für die andere Sonne gelten muss, wenn das System in ewiger Balance sein soll. Durch den Drehpunkt F0 spiegelt sich die Bahn der ersten Sonne genau auf die Bahn der zweite Sonne. Und das galt ganz genauso auch für unser Beispiel aus Bild 3. Bild 4: Sonne umkreist Sonne auf zwei elliptischen Bahnen Kommen wir als letztes Beispiel nun zu deutlicheren Masseunterschieden, z.B. ein Planet, der seine Sonne auf einer elliptischen Bahn umkreist oder ein Asteroid, der um eine Sonne fliegt. Bild 5: Planet umkreist Sonne auf elliptischer Bahn Und was wäre, wenn der Planet zwenig Schwung hätte und am äußeren Scheitelpunkt ganz stehen bliebe? Das ist natürlich eine Fangfrage! Weil, wer aufgepasst hat, weiss bereits, dass v, um den Bahnorbit zu halten, immer so groß sein muss, dass Flieh- und Anziehungskraft sich genau kompensieren (balanciertes System). Der Planet käme also überhaupt nicht bis an den Scheitelpunkt, da er schon vorher, wie das zu langsame Auto auf einer Carrera Bahn aus dem Looping fällt. Die beiden Massen ziehen sich ja an und würden bei zu geringem v gleich aufeinander zufliegen, aber das v macht da halt vorher einen Bogen draus, zuwenig v heißt zuviel Bogen, zuviel v ergibt zuwenig Bogen, was den Planeten aus seiner Bahn ausscheren lässt. Zurück zum Index